5.2.12. nvector.core.n_EB_E2p_EB_E

n_EB_E2p_EB_E(n_EB_E, depth=0, a=6378137, f=0.0033528106647474805, R_Ee=None)

Converts n-vector to Cartesian position vector in meters.

Parameters

n_EB_E: 3 x n array

n-vector(s) [no unit] of position B, decomposed in E.

depth: 1 x n array

Depth(s) [m] of system B, relative to the ellipsoid (depth = -height)

a: real scalar, default WGS-84 ellipsoid.

Semi-major axis of the Earth ellipsoid given in [m].

f: real scalar, default WGS-84 ellipsoid.

Flattening [no unit] of the Earth ellipsoid. If f==0 then spherical Earth with radius a is used in stead of WGS-84.

R_Ee3 x 3 array

rotation matrix defining the axes of the coordinate frame E.

Returns

p_EB_E: 3 x n array

Cartesian position vector(s) from E to B, decomposed in E.

See also

p_EB_E2n_EB_E, n_EA_E_and_p_AB_E2n_EB_E, n_EA_E_and_n_EB_E2p_AB_E

Notes

The position of B (typically body) relative to E (typically Earth) is given into this function as n-vector, n_EB_E. The function converts to cartesian position vector (“ECEF-vector”), p_EB_E, in meters. The calculation is exact, taking the ellipsity of the Earth into account. It is also non-singular as both n-vector and p-vector are non-singular (except for the center of the Earth). The default ellipsoid model used is WGS-84, but other ellipsoids/spheres might be specified.

Examples

Example 4: “Geodetic latitude to ECEF-vector”

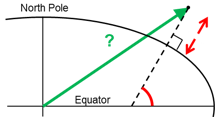
Geodetic latitude, longitude and height are given for position B as latEB, lonEB and hEB, find the ECEF-vector for this position, p_EB_E.

Solution:

>>> import nvector as nv
>>> from nvector import rad
>>> wgs84 = dict(a=6378137.0, f=1.0/298.257223563)
>>> lat_EB, lon_EB = rad(1), rad(2)
>>> h_EB = 3
>>> n_EB_E = nv.lat_lon2n_E(lat_EB, lon_EB)
>>> p_EB_E = nv.n_EB_E2p_EB_E(n_EB_E, -h_EB, **wgs84)

>>> 'Ex4: p_EB_E = {} m'.format(p_EB_E.ravel().tolist())
'Ex4: p_EB_E = [6373290.277218279, 222560.20067473652, 110568.82718178593] m'